こんにちは、SSLに新たに加わりました、 北海道大学 青木です。どうぞよろしくお願いします。
SSLでは「音の技術」というとデータ通信関連の話題が多めですが、今回は少し趣向を変えて、別の音の技術である「音声の合成」についてお話ししたいと思います。
最近は、スマートスピーカーの登場もあいまって、合成音声を耳にする機会が多くなってきましたが、そもそもコンピュータはどうやって音声を合成しているのか、皆さんはご存知でしょうか。
音声合成の土台になっているのは、実際に人間が音声を生成するしくみを観察することで構築されたソース・フィルタ理論と呼ばれる考え方です。図1に示すように、周期的複合音である声帯音源をソースとし、フォルマントによって特徴づけられる声道をフィルタとすることで、音声の生成のしくみを説明しているのが、ソース・フィルタ理論の考え方にほかなりません。
もう少し噛み砕いて説明します。「声」を含めて、あらゆる音は、さまざまに違う周波数(高さ)の音波が重なり合ったものとして捉えることができます。そして、「どの周波数の音がどのくらい強く出ているか」というバランスの違いを、私たちは「音色の違い」として捉えるのです。ちなみに、図1(a)のように、全ての周波数帯で同じくらいの音量が出ている音を「ホワイトノイズ」と呼びますが、これはテレビが映っていない時に聴こえる「ザー」というあの音です。
フォルマントというのは、人間の声に含まれる周波数帯のバランスを分析した時に、音色の特徴を決定づける、他の帯域に比べて特に強く出ている周波数のピークのことを言います。
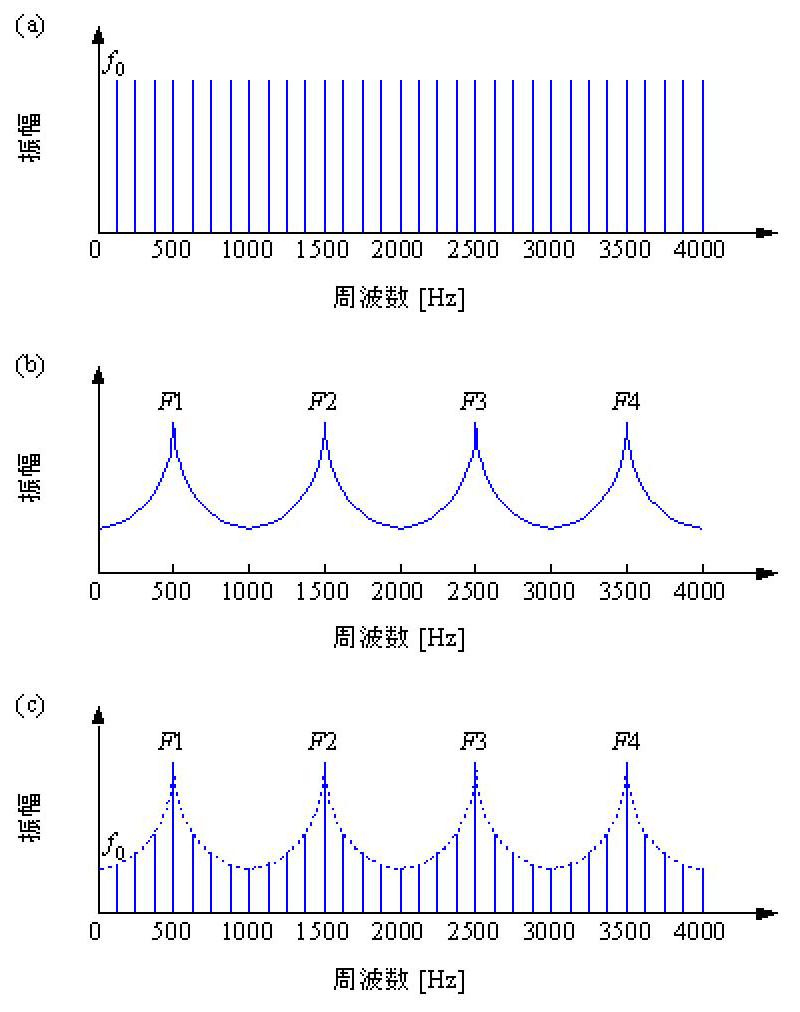
図1 ソース・フィルタ理論:(a) 声帯音源(ソース), (b) 声道(フィルタ), (c) 音声
フォルマントは声道の形状によって変化します。また、声道の形状はそれぞれの母音ごとに変化します。そのため、図2に示すように、それぞれの母音ごとにフォルマントは変化することになります。
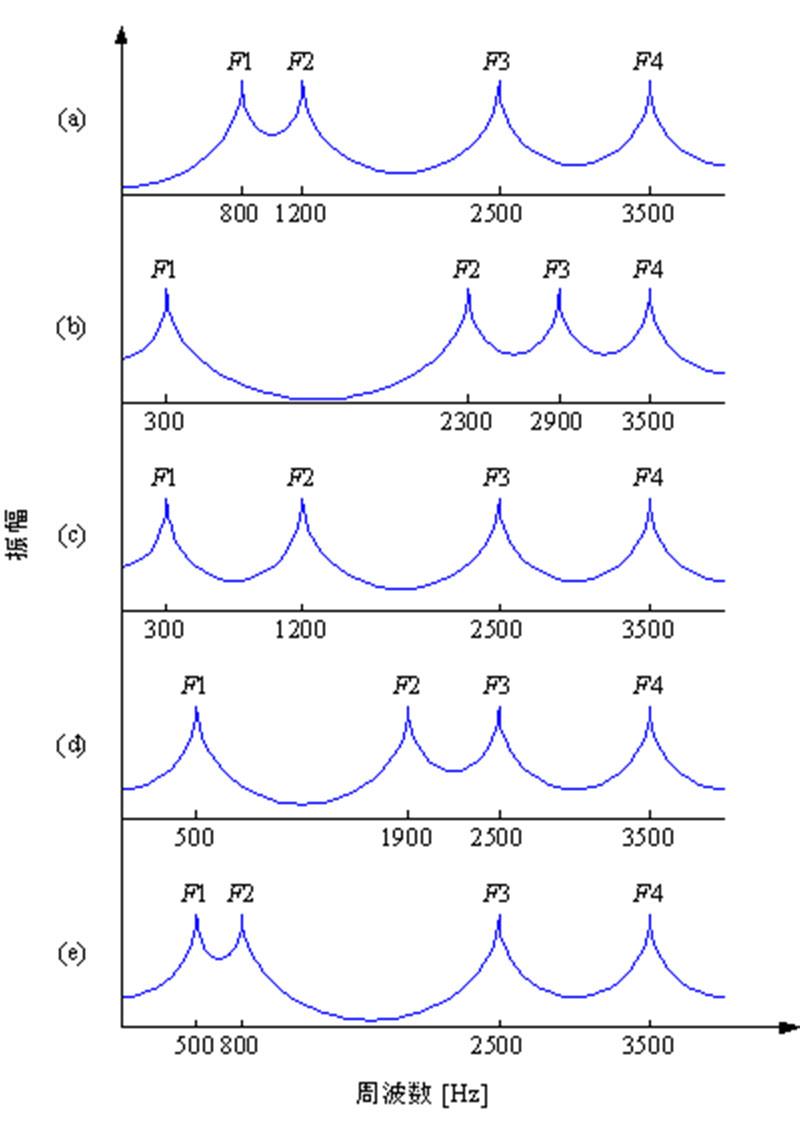
図2 声道の周波数特性:(a)「ア」, (b)「イ」, (c)「ウ」, (d)「エ」, (e)「オ」
こうしたフォルマントのなかで、母音の知覚に大きな影響をおよぼしているのが、第1フォルマント周波数F1と第2フォルマント周波数F2です。図3に示すように、これらを2次元平面にプロットしたF1-F2ダイアグラムを観察すると、それぞれの母音を識別することができます。じつは、これが音声認識の原理になっています。
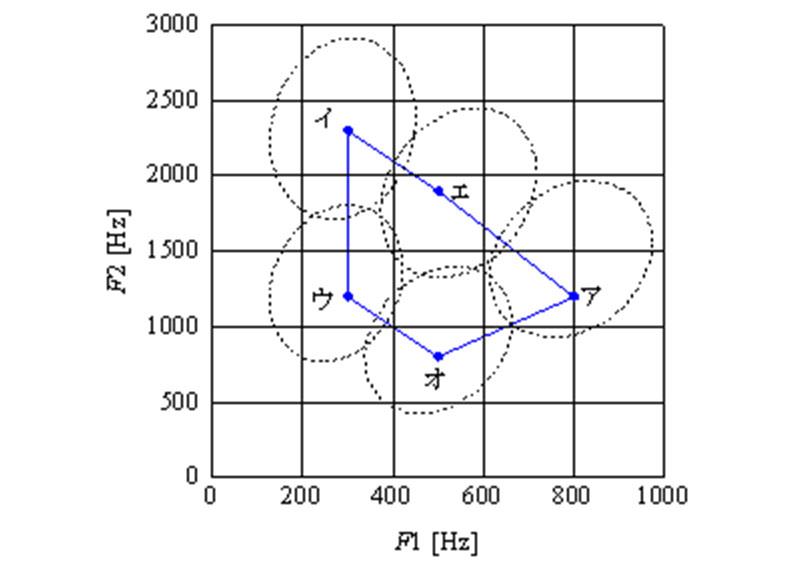
図3 F1-F2ダイアグラム
逆に、こうしたフォルマントを再現することが、音声合成の原理になっています。特定の帯域の周波数成分だけを通過させるBPF(帯域通過フィルタ)を使ってフォルマントを再現すると、それぞれの母音を合成することができます。図4に示すように、BPFは、fc(中心周波数)とB(帯域幅)と呼ばれるパラメータによって定義することができます。
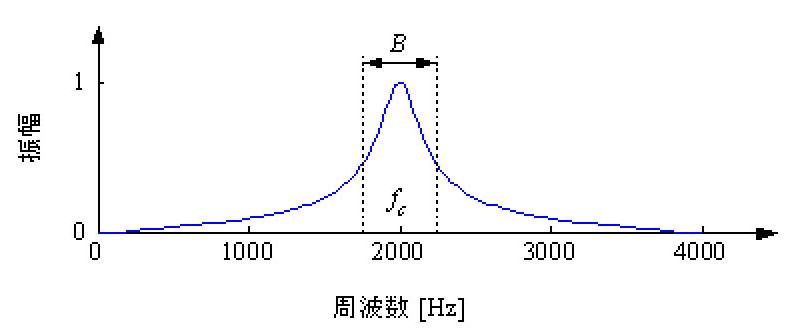
図4 BPFの周波数特性
実際に、音声合成を行ってみることにしましょう。ここでは、基本周波数125Hzのパルス列 pulse_train.wav を入力信号にしてみます。このパルス列に対して、母音「ア」のフォルマントを再現すると、出力信号は a.wav になります。a.wavを聞いてみると、母音「ア」のように聞こえることがおわかりいただけるでしょうか。
pulse_train.wav
a.wav
図5に示すように、パルス列に複数のBPFをかけると、波形は複雑に変化することになります。このように、本来は単純なブザーにしか聞こえないパルス列も、フィルタを使って周波数特性を加工すると、音声のような複雑な音に変化させることができます。
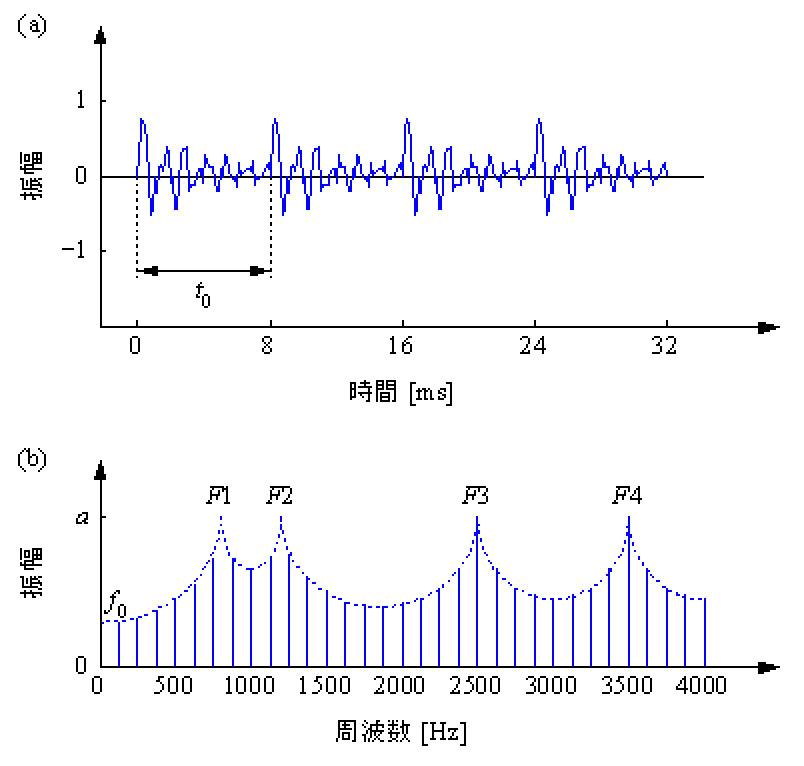
図5 母音「ア」の合成音声:(a) 波形, (b) 周波数特性
ソース・フィルタ理論にもとづく音声合成の原理は、さまざまな楽器音を合成するシンセサイザーにも共通するしくみになっており、減算合成と呼ばれるテクニックとして広く利用されています。サウンドプログラミングでは、音声合成をはじめとする音響合成が重要なテーマになっていますが、フィルタを使って周波数特性を加工することはそのための重要なアプローチになっています。